Należy napisać program pozwalający na przetwarzanie obrazów
cyfrowych. Program ma prezentować użytkownikowi menu,
pozwalające na:
- wybór pliku zawierającego obraz przeznaczony do obróbki,
- wykonanie wybranych operacji na obrazie zgodnie z zaleceniem
prowadzącego zajęcia (skalowanie, zamiana formatu obrazu,
konturowanie, nakładanie obrazów itp.) -- opis możliwych operacji
na obrazie znajduje się poniżej.
- zapisanie przetworzonego obrazu na pliku,
- wyświetlenie obrazu (początkowego lub po obróbce) na ekranie,
w celu szybkiej weryfikacji wyniku,
- zakończenie działania programu.
- Program będzie operował na wskazanych przez prowadzącego
formatach plików. Opis możliwych formatów plików znajduje się na
stronie
![[*]](crossref.png) .
.
- W celu wizualizacji obraz będzie wyświetlany przy wykorzystaniu
programu xv (wywoływanego funkcją C
system).
- Program musi zostać wyposażony w interfejs użytkownika zbudowany
w oparciu o bibliotekę curses (więcej o interfejsach użytkownika na
stronie
![[*]](crossref.png) ). W przypadku implementacji większej
niż wymagana liczby operacji na obrazie/obsługi większej liczby
formatów plików postać interfejsu jest dowolna.
). W przypadku implementacji większej
niż wymagana liczby operacji na obrazie/obsługi większej liczby
formatów plików postać interfejsu jest dowolna.
W rozliczeniu ćwiczenia należy dostarczyć program napisany w pascalu.
Operacje na obrazie
Obrazy cyfrowe są na ogół dwuwymiarowymi tablicami złożonymi
z pikseli, które to piksele reprezentowane są przez liczby określające
ich jasność i kolor, a uzyskiwane na przykład z kamery podłączonej do
komputera. Ważnym zagadnieniem w technice jest rozpoznawanie takich
obrazów, to znaczy ustalenie, który fragment obrazu odpowiada któremu
obiektowi rzeczywistemu, i jakie informacje o tym obiekcie możemy
uzyskać, np. jego położenie, kierunek ruchu, prędkość. Jest to
zadanie trudne, szczególnie ze względu na fakt, że obrazy otrzymywane
z kamer zawierają oprócz obrazów interesujących obiektów dużą ilość
innych informacji i są dodatkowo zmodyfikowane takimi zjawiskami jak:
natężenie i kolor oświetlenia, ilość, rozmieszczenie i charakter
źródeł światła, odbicia, nieostrość, różnice w obrazie obiektu w
zależności od odległości i orientacji, oraz innymi. Dlatego, proces
analizy obrazu rozbija się na szereg operacji prostszych, takich jak
wstępna filtracja, skalowanie, konturowanie, wyodrębnienie obiektów
itd.
W niektórych zastosowaniach celowe jest sztuczne wyostrzanie konturów
(obrysów poszczególnych elementów obrazów) w celu wydobycia
szczegółów, prowadzące w krańcowym przypadku do przekształcenia obrazu
do postaci dwupoziomowej, z zaznaczonymi wyłącznie konturami. Poniżej
zajmiemy się konturowaniem obrazów monochromatycznych. Jedną z metod
wyodrębniania konturów obrazu jest metoda gradientowa.
Gradient funkcji jest funkcją wektorową przyporządkowującą każdemu
punktowi wektor wskazujący kierunek największego wzrostu funkcji
podstawowej, o wartości proporcjonalnej do wielkości tego wzrostu.
Jeżeli funkcją podstawową 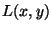 będzie funkcja jasności obrazu
monochromatycznego (czarno-białego), to miejsca o dużych wartościach
gradientu, czyli zmiany jasności, odpowiadają często konturom obiektów
widocznych na obrazie.
będzie funkcja jasności obrazu
monochromatycznego (czarno-białego), to miejsca o dużych wartościach
gradientu, czyli zmiany jasności, odpowiadają często konturom obiektów
widocznych na obrazie.
Moduł gradientu funkcji jasności jest dany wzorem:
Dla zapisanego w dwuwymiarowej tablicy ![$ L[x,y]$](img3.png) monochromatycznego
obrazu cyfrowego możemy różniczki zupełne z powyższego wzoru
zastąpić w przybliżeniu zwykłymi różnicami. Wzór przybiera wtedy
postać:
monochromatycznego
obrazu cyfrowego możemy różniczki zupełne z powyższego wzoru
zastąpić w przybliżeniu zwykłymi różnicami. Wzór przybiera wtedy
postać:
Z kolei, ponieważ przy konturowaniu istotny jest tylko
bezwzględny przyrost wartości funkcji jasności, możemy
skorzystać z wzoru uproszczonego, w którym pierwiastek sumy
kwadratów zastąpiono sumą wartości bezwzględnych:
Oba powyższe wzory różnicowe można obliczyć dla wszystkich punktów
obrazu, oczywiście za wyjątkiem punktów z ostatniego rzędu i
ostatniej kolumny obrazu, co wynika to z przyjętego sposobu
przybliżania różnic.
Skalowanie polega na zmianie liczby pikseli tworzących obraz. Przy
skali 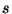 z obrazu wyjściowego o wymiarach
z obrazu wyjściowego o wymiarach 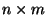 otrzymujemy
obraz o wymiarach
otrzymujemy
obraz o wymiarach
![$ [s\ast n]\times [s\ast m]$](img8.png) , gdzie
, gdzie ![$ [x]$](img9.png) oznacza
część całkowitą liczby
oznacza
część całkowitą liczby 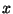 . Poniżej zostanie opisana metoda
skalowania obrazów monochromatycznych dla skal całkowitych
(powiększanie) i o wartościach
. Poniżej zostanie opisana metoda
skalowania obrazów monochromatycznych dla skal całkowitych
(powiększanie) i o wartościach 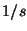 ,
,
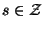 (pomniejszanie). Dla jasności punktu obrazu wyjściowego danego
funkcją
(pomniejszanie). Dla jasności punktu obrazu wyjściowego danego
funkcją 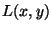 obraz wynikowy będzie opisany przez
obraz wynikowy będzie opisany przez
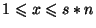 ,
,
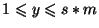 , przy powiększaniu (skala
, przy powiększaniu (skala 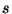 ) oraz przez
) oraz przez
![$ 1\le x\le [n/{}s]$](img17.png) ,
,
![$ 1\le y\le [m/{}s]$](img18.png) , przy pomniejszaniu (skala
, przy pomniejszaniu (skala
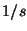 ). Widać, że przy takim wyborze funkcji skalowanie polega na
powielaniu/pomijaniu punktów obrazu wyjściowego. Oczywiście
możliwy jest inny wybór funkcji, przy których np. jasność
punktów obrazu wynikowego wyliczana jest jako średnia jasności
sąsiadujących ze sobą punktów obrazu wyjściowego.
). Widać, że przy takim wyborze funkcji skalowanie polega na
powielaniu/pomijaniu punktów obrazu wyjściowego. Oczywiście
możliwy jest inny wybór funkcji, przy których np. jasność
punktów obrazu wynikowego wyliczana jest jako średnia jasności
sąsiadujących ze sobą punktów obrazu wyjściowego.
Zamiana obrazu kolorowego na monochromatyczny polega na wyliczeniu dla
każdego piksela obrazu wyjściowego jego jasności na podstawie
informacji o jego składowych kolorowych 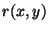 ,
, 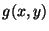 ,
, 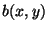 .
Najprościej można tego dokonać stosując wzór
.
Najprościej można tego dokonać stosując wzór
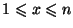 ,
,
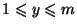 . Przy dokonywaniu procesu odwrotnego
(zamianie obrazu monochromatycznego na kolorowy) najprościej jest
przyjąć wartość jasności poszczególnych punktów jako wartości
nasycenia ich składowych kolorowych (naturalnie nie zmieni to
wyglądu obrazu -- zmianie ulegnie jedynie sposób jego reprezentacji).
. Przy dokonywaniu procesu odwrotnego
(zamianie obrazu monochromatycznego na kolorowy) najprościej jest
przyjąć wartość jasności poszczególnych punktów jako wartości
nasycenia ich składowych kolorowych (naturalnie nie zmieni to
wyglądu obrazu -- zmianie ulegnie jedynie sposób jego reprezentacji).
Jedną z metod segmentacji obrazu jest progowanie. Polega ono na
dokonaniu klasyfikacji pikseli obrazu do jednej z dwóch klas: zbioru
punktów czarnych lub zbioru punktów białych. Proces może zostać
przeprowadzony po arbitralnym wybraniu wartości progu 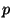 zgodnie ze
wzorem
zgodnie ze
wzorem
Przedstawione operacje na obrazie nie wyczerpują oczywiście
wachlarza możliwych sposobów przetwarzania obrazów. Ponadto
możliwe jest łączenie kilku obrazów ze sobą, wycinanie
fragmentów obrazu, obracanie obrazu, zmiana jego jasności,
kontrastu, zabarwienia, solaryzacja, rozmywanie, wyostrzanie itp.
Reprezentacja obrazu
Obrazy pobierane z kamery, bądź dowolnego innego źródła, mogą
być składowane na pliku dyskowym w jednym z wielu istniejących
formatów zapisu obrazów rastrowych. Poniżej omówiono kilka z
nich.
Przenośny format bitmapowy pbm (portable bitmap) jest to
najprostszy format monochromatyczny (z pewnością dużo prostszy od
jego opisu:-). Nadaje się on do przechowywania
obrazów czarno-białych (sensu stricte, tzn. złożonych jedynie z
pikseli czarnych lub białych). W podstawowej wersji tworzony plik
jest plikiem tekstowym zawierającym informacje o pojedynczym obrazie.
Plik zapisany w formacie pbm zawiera w kolejności:
- ,,Numer magiczny'', określający rodzaj pliku. Numer magiczny
najprostszego pliku pbm to dwa pierwsze znaki, ustawione na ,,P1''.
- Co najmniej jeden znak biały (spacja, tabulacja, CR, LF).
- Szerokość obrazu (
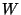 ), podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
), podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
- Co najmniej jeden znak biały.
- Wysokość obrazu (
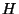 ), znowu podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
), znowu podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
- Co najmniej jeden znak biały.
- Ciąg
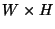 znaków ,,
znaków ,,0'' lub
,,1''. Znak ,,0'' oznacza biel, znak ,,1''
oznacza czerń. Znaki kodują piksele obrazu począwszy od jego
lewego górnego rogu w kierunku zgodnym z kierunkiem normalnego
czytania. Znaki białe w tej sekcji są ignorowane.
- Cokolwiek zaczynające się od białego znaku -- zostanie to zignorowane.
- Linia zawierająca informacje o szerokości obrazu może być
poprzedzona liniami komentarza rozpoczynającymi się znakiem ,,
#''
-- linie te są ignorowane.
- Linie nie powinny być dłuższe niż 70 znaków.
Oto przykład małej bitmapy w tym formacie:
P1
# feep.pbm
24 7
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 1 1 1 1 0 0 1 1 1 1 0 0 1 1 1 1 0 0 1 1 1 1 0
0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 1 0
0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 0 0 0 1 1 1 1 0
0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 0
0 1 0 0 0 0 0 1 1 1 1 0 0 1 1 1 1 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
która definiuje obraz o rozmiarach
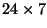 pikseli. Proszę
zauważyć, że graficzny układ pliku nie musi odzwierciedlać w
żaden sposób układu obrazka (wszystkie znaki mogą być podane w
jednej linii, bądź każdy znak może znaleźć się w osobnej
linii, czy jakkolwiek inaczej).
pikseli. Proszę
zauważyć, że graficzny układ pliku nie musi odzwierciedlać w
żaden sposób układu obrazka (wszystkie znaki mogą być podane w
jednej linii, bądź każdy znak może znaleźć się w osobnej
linii, czy jakkolwiek inaczej).
Istnieje wariant tego formatu pozwalający na zapisanie informacji o
pikselach obrazu w postaci binarnej. Różnice pomiędzy tym formatem
a formatem opisanym wcześniej to:
- ,,Numer magiczny'', to ,,P4'' zamiast ,,P1''.
- Po wysokości
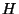 dozwolony jest tylko jeden znak biały (zazwyczaj
znak nowej linii).
dozwolony jest tylko jeden znak biały (zazwyczaj
znak nowej linii).
- Ciąg
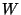 rzędów zawierających po nie mniej niż
rzędów zawierających po nie mniej niż 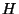 bitów,
występujący w miejscu ciągu znaków ,,
bitów,
występujący w miejscu ciągu znaków ,,0'' lub
,,1''. Każdy bit koduje pojedynczy piksel obrazu tak, jak
poprzednio robiły to znaki. Bity są zapisywane po osiem na bajt, w
kolejności najpierw bardziej znaczący. Ostatni bajt w każdym
rzędzie uzupełniony jest w razie potrzeby bitami nieznaczącymi.
Nie są dopuszczalne w tej sekcji białe znaki.
- Plik może zawierać informacje o kilku następujących po sobie
obrazach.
Więcej -- man pbm.
Formaty plików pgm
Przenośny format szarej bitmapy pgm (portable graymap) jest to
prosty format monochromatyczny. Nadaje się on do przechowywania
obrazów zawierających wiele odcieni szarości. W podstawowej wersji
tworzony plik jest plikiem tekstowym zawierającym informacje o
pojedynczym obrazie. Plik zapisany w formacie pgm zawiera w
kolejności:
- ,,Numer magiczny'', określający rodzaj pliku. Numer magiczny
tekstowej wersji pliku pgm to dwa pierwsze znaki, ustawione na ,,P2''.
- Co najmniej jeden znak biały (spacja, tabulacja, CR, LF).
- Szerokość obrazu (
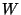 ), podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
), podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
- Co najmniej jeden znak biały.
- Wysokość obrazu (
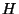 ), znowu podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
), znowu podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
- Co najmniej jeden znak biały.
- Maksymalna wartość szarości (
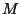 ), również podana jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
), również podana jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
- Co najmniej jeden znak biały.
- Ciąg
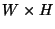 wartości zawierających się między 0 a
wartości zawierających się między 0 a 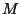 i zapisanych jako liczby dziesiętne w kodzie ASCII odzielone od
siebie białymi znakami. 0 oznacza czerń,
i zapisanych jako liczby dziesiętne w kodzie ASCII odzielone od
siebie białymi znakami. 0 oznacza czerń, 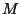 -- biel,
pozostałe wartości -- odcienie pośrednie. Wartości kodują piksele
obrazu począwszy od jego lewego górnego rogu w kierunku zgodnym z
kierunkiem normalnego czytania.
-- biel,
pozostałe wartości -- odcienie pośrednie. Wartości kodują piksele
obrazu począwszy od jego lewego górnego rogu w kierunku zgodnym z
kierunkiem normalnego czytania.
- Linia zawierająca informacje o maksymalnej wartości szarości obrazu może być
poprzedzona liniami komentarza rozpoczynającymi się znakiem ,,
#''
-- linie te są ignorowane.
- Linie nie powinny być dłuższe niż 70 znaków.
Oto przykład małej bitmapy w tym formacie:
P2
# feep.pgm
24 7
15
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 3 3 3 3 0 0 7 7 7 7 0 0 11 11 11 11 0 0 15 15 15 15 0
0 3 0 0 0 0 0 7 0 0 0 0 0 11 0 0 0 0 0 15 0 0 15 0
0 3 3 3 0 0 0 7 7 7 0 0 0 11 11 11 0 0 0 15 15 15 15 0
0 3 0 0 0 0 0 7 0 0 0 0 0 11 0 0 0 0 0 15 0 0 0 0
0 3 0 0 0 0 0 7 7 7 7 0 0 11 11 11 11 0 0 15 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
która jak poprzednio definiuje obraz o rozmiarach
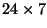 pikseli, zawierający 15 odcieni szarości. I tutaj graficzny układ
pliku nie musi odzwierciedlać w żaden sposób układu obrazka
(wszystkie liczby mogą być podane w jednej linii, bądź każda
liczba może znaleźć się w osobnej linii, czy jakkolwiek inaczej).
pikseli, zawierający 15 odcieni szarości. I tutaj graficzny układ
pliku nie musi odzwierciedlać w żaden sposób układu obrazka
(wszystkie liczby mogą być podane w jednej linii, bądź każda
liczba może znaleźć się w osobnej linii, czy jakkolwiek inaczej).
Istnieje także wariant tego formatu pozwalający na zapisanie
informacji o pikselach obrazu w postaci binarnej. Różnice pomiędzy
tym formatem a formatem opisanym wcześniej to:
- ,,Numer magiczny'', to ,,P5'' zamiast ,,P2''.
- Maksymalna wartość szarości musi być mniejsza od 65536.
- Po maksymalnej wartości szarości
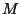 dozwolony jest tylko jeden znak biały (zazwyczaj
znak nowej linii).
dozwolony jest tylko jeden znak biały (zazwyczaj
znak nowej linii).
- Ciąg
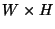 wartości zawierających się między 0 a
wartości zawierających się między 0 a 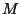 i zapisanych binarnie za pomocą jednego (dla
i zapisanych binarnie za pomocą jednego (dla 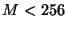 ) lub dwóch
bajtów (bardziej znaczący bajt jest pierwszy). Sposób kodowania pikseli jak poprzednio.
Nie są dopuszczalne w tej sekcji białe znaki.
) lub dwóch
bajtów (bardziej znaczący bajt jest pierwszy). Sposób kodowania pikseli jak poprzednio.
Nie są dopuszczalne w tej sekcji białe znaki.
- Plik może zawierać informacje o kilku następujących po sobie
obrazach.
Więcej -- man pgm.
Przenośny format pixmapowy ppm (portable pixmap) jest to prosty
format dla obrazów kolorowych. Należy zaznaczyć, że format ten
jest wysoce nie efektywny, powoduje tworzenie ogromnych plików,
zawierających niejednokrotnie informacje o obrazie, których oko
ludzkie w ogóle nie jest w stanie dostrzec. Jednakże prostota tego
formatu decyduje o jego stosowaniu. W podstawowej wersji tworzony plik
jest plikiem tekstowym zawierającym informacje o pojedynczym obrazie.
Plik zapisany w formacie ppm zawiera w kolejności:
- ,,Numer magiczny'', określający rodzaj pliku. Numer magiczny
tekstowej wersji pliku ppm to dwa pierwsze znaki, ustawione na ,,P3''.
- Co najmniej jeden znak biały (spacja, tabulacja, CR, LF).
- Szerokość obrazu (
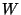 ), podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
), podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
- Co najmniej jeden znak biały.
- Wysokość obrazu (
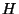 ), znowu podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
), znowu podana w pikselach jako liczba dziesiętna zapisana za
pomocą znaków ASCII.
- Co najmniej jeden znak biały.
- Maksymalna wartość składowych kolorowych obrazu (
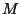 ),
również podana jako liczba dziesiętna zapisana za pomocą znaków
ASCII.
),
również podana jako liczba dziesiętna zapisana za pomocą znaków
ASCII.
- Co najmniej jeden znak biały.
- Ciąg
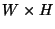 trójek wartości zawierających się między
0 a
trójek wartości zawierających się między
0 a 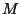 i zapisanych jako liczby dziesiętne w kodzie ASCII,
oddzielone od siebie białymi znakami. Kolejne trzy wartości
oznaczają poziom składowej czerwonej, zielonej i niebieskiej dla
poszczególnych pikseli. 0 oznacza wyłączenie koloru,
i zapisanych jako liczby dziesiętne w kodzie ASCII,
oddzielone od siebie białymi znakami. Kolejne trzy wartości
oznaczają poziom składowej czerwonej, zielonej i niebieskiej dla
poszczególnych pikseli. 0 oznacza wyłączenie koloru, 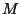 --
jego maksymalne nasycenie. Trójki kodują piksele obrazu począwszy
od jego lewego górnego rogu w kierunku zgodnym z kierunkiem
normalnego czytania.
--
jego maksymalne nasycenie. Trójki kodują piksele obrazu począwszy
od jego lewego górnego rogu w kierunku zgodnym z kierunkiem
normalnego czytania.
- Linia zawierająca informacje o maksymalnej wartości
składowych kolorowych obrazu może być
poprzedzona liniami komentarza rozpoczynającymi się znakiem ,,
#''
-- linie te są ignorowane.
- Linie nie powinny być dłuższe niż 70 znaków.
Oto przykład małej bitmapy w tym formacie:
P3
# feep.ppm
4 4
15
0 0 0 0 0 0 0 0 0 15 0 15
0 0 0 0 15 7 0 0 0 0 0 0
0 0 0 0 0 0 0 15 7 0 0 0
15 0 15 0 0 0 0 0 0 0 0 0
która definiuje obraz o rozmiarach 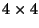 pikseli. Ponownie
graficzny układ pliku nie musi odzwierciedlać w żaden sposób
układu obrazka (wszystkie liczby mogą być podane w jednej linii,
bądź każda liczba może znaleźć się w osobnej linii, czy
jakkolwiek inaczej).
pikseli. Ponownie
graficzny układ pliku nie musi odzwierciedlać w żaden sposób
układu obrazka (wszystkie liczby mogą być podane w jednej linii,
bądź każda liczba może znaleźć się w osobnej linii, czy
jakkolwiek inaczej).
Istnieje także wariant tego formatu pozwalający na zapisanie
informacji o pikselach obrazu w postaci binarnej. Różnice pomiędzy
tym formatem a formatem opisanym wcześniej to:
- ,,Numer magiczny'', to ,,P6'' zamiast ,,P3''.
- Maksymalna wartość składowych kolorowych musi być mniejsza od 65536.
- Po maksymalnej wartości składowych kolorowych
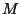 dozwolony jest tylko jeden znak biały (zazwyczaj
znak nowej linii).
dozwolony jest tylko jeden znak biały (zazwyczaj
znak nowej linii).
- Ciąg
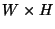 trójek zawierających się między 0 a
trójek zawierających się między 0 a 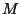 i
zapisanych binarnie za pomocą jednego (dla
i
zapisanych binarnie za pomocą jednego (dla 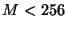 ) lub dwóch
bajtów (bardziej znaczący bajt jest pierwszy). Sposób kodowania
pikseli jak poprzednio. Nie są dopuszczalne w tej sekcji białe
znaki.
) lub dwóch
bajtów (bardziej znaczący bajt jest pierwszy). Sposób kodowania
pikseli jak poprzednio. Nie są dopuszczalne w tej sekcji białe
znaki.
- Plik może zawierać informacje o kilku następujących po sobie
obrazach.
Więcej -- man ppm.
Częstokroć istnieje potrzeba zmiany formatu pliku, w którym zapisany
został obraz. W najlepszym wypadku czynność ta wymaga odczytania
zawartości konwertowanego pliku, przekształceniu formatu na docelowy i
zapisaniu całości ponownie na plik. Tak będzie np. przy zamianie
obrazu czarno-białego na obraz o 15-stu stopniach szarości, czy obrazu
zawierającego 15 stopni szarości na obraz o 256-ciu stopniach
szarości. Jednakże przy konwersji w drugą stronę (z 256-ciu stopni
szarości na 15, czy z 15-stu na 2) wymagane jest wykonanie odpowiednich
operacji na samym obrazie (ponieważ format docelowy pozwala na
przechowanie mniejszej ilości informacji o obrazie niż format
wyjściowy). Może dodatkowo pojawić się potrzeba progowania obrazu,
zmniejszenia liczby zawartych w nim poziomów szarości, konwersji
obrazu kolorowego do obrazu monochromatycznego.
Oczywiście istnieje wiele innych formatów plików służących do
przechowywania obrazów cyfrowych, jak chociażby popularne formaty jpeg (joint photographic experts group), gif (graphics
interchange format), tiff (tag image file format) czy bmp
(MS-Windows bitmap format).
Interfejs użytkownika
Każdy program przewidziany do interaktywnego wykorzystania przez
użytkownika posiada interfejs użytkownika. Interferjs ten może przyjąć
postać sekwencji zadawanych pytań, po których następuje realizacja
zadania, prostego tekstowego menu, z którego użytkownik może wybrać
pożądane operacje, czy w końcu zaawansowanego interfejsu graficznego,
z całą paletą rozwijalnych menu, zakładek i tym podobnych elementów.
Zazwyczaj najprostsze menu tekstowe programista tworzy nie
wykorzystując żadnych dodatkowych narzędzi, zaś do budowy menu okienkowych
czy graficznych wspomaga się odpowiednimi bibliotekami i innymi
narzędziami. W systemie unix do budowy tekstowych menu okienkowych
służy biblioteka curses. Ponadto interfejs użytkownika może
stanowić integralną cześć programu lub może być samodzielnym
programem. W drugim z wymienionych przypadków może go stanowić skrypt
interpretowany przez jedną z dostępnych w uniksie powłok (powłokę Bourne shell, język skryptowy Tcl, pakiet okienkowy Tk).
This document was generated using the
LaTeX2HTML translator Version 2K.1beta (1.48)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -html_version 3.2,latin2,unicode -split 0 Obrazy_pgm
The translation was initiated by Robert Muszyński on 2003-04-02
Robert Muszyński
2003-04-02
![[*]](crossref.png) .
.
![[*]](crossref.png) ). W przypadku implementacji większej
niż wymagana liczby operacji na obrazie/obsługi większej liczby
formatów plików postać interfejsu jest dowolna.
). W przypadku implementacji większej
niż wymagana liczby operacji na obrazie/obsługi większej liczby
formatów plików postać interfejsu jest dowolna.
![[*]](crossref.png) .
.
![[*]](crossref.png) ). W przypadku implementacji większej
niż wymagana liczby operacji na obrazie/obsługi większej liczby
formatów plików postać interfejsu jest dowolna.
). W przypadku implementacji większej
niż wymagana liczby operacji na obrazie/obsługi większej liczby
formatów plików postać interfejsu jest dowolna.
![]() będzie funkcja jasności obrazu
monochromatycznego (czarno-białego), to miejsca o dużych wartościach
gradientu, czyli zmiany jasności, odpowiadają często konturom obiektów
widocznych na obrazie.
będzie funkcja jasności obrazu
monochromatycznego (czarno-białego), to miejsca o dużych wartościach
gradientu, czyli zmiany jasności, odpowiadają często konturom obiektów
widocznych na obrazie.
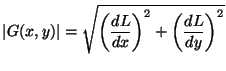
![]() monochromatycznego
obrazu cyfrowego możemy różniczki zupełne z powyższego wzoru
zastąpić w przybliżeniu zwykłymi różnicami. Wzór przybiera wtedy
postać:
monochromatycznego
obrazu cyfrowego możemy różniczki zupełne z powyższego wzoru
zastąpić w przybliżeniu zwykłymi różnicami. Wzór przybiera wtedy
postać:
![]() z obrazu wyjściowego o wymiarach
z obrazu wyjściowego o wymiarach ![]() otrzymujemy
obraz o wymiarach
otrzymujemy
obraz o wymiarach
![]() , gdzie
, gdzie ![]() oznacza
część całkowitą liczby
oznacza
część całkowitą liczby ![]() . Poniżej zostanie opisana metoda
skalowania obrazów monochromatycznych dla skal całkowitych
(powiększanie) i o wartościach
. Poniżej zostanie opisana metoda
skalowania obrazów monochromatycznych dla skal całkowitych
(powiększanie) i o wartościach ![]() ,
,
![]() (pomniejszanie). Dla jasności punktu obrazu wyjściowego danego
funkcją
(pomniejszanie). Dla jasności punktu obrazu wyjściowego danego
funkcją ![]() obraz wynikowy będzie opisany przez
obraz wynikowy będzie opisany przez
![]() ,
, ![]() ,
, ![]() .
Najprościej można tego dokonać stosując wzór
.
Najprościej można tego dokonać stosując wzór
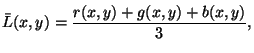
![]() zgodnie ze
wzorem
zgodnie ze
wzorem